Prefix

Microsoft Fax is the Fax service included with Windows. In Windows 2000, XP and 2003 it is controlled by the "Send Fax Wizard", while in Windows 10/8/7/Vista and Server 2008/2012 it is controlled by "Windows Fax and Scan".

NetModem allows accessing shared modems over a network. The PC containing the modem(s) runs the NetModem Server software, and the PC's needing to access the modem(s) runs NetModem Client software, which allows modem or fax applications to access the remote modems as if they were locally connected.

When using the Microsoft Fax service on a NetModem Client PC to control a fax modem located on a NetModem Server PC, it is recommended to configure Microsoft Fax to use Fax Class 2 or Class 2.x if the modem(s) supports it.

Fax Class 1 is a software driven protocol, which uses the local computers CPU to perform session management. When Fax Class 1 is used over a networked modem, the timing can be slightly off due to network latency, which can sometimes cause a fax session to fail or distort.

Fax Class 2 uses the fax modems hardware to perform session management, so it should always work reliably over a networked modem.

Fax Class 2.0 is similar in concept to Fax Class 2, but it is a different protocol which has been documented and approved by the ITU. It is not as commonly used as Class 2.

Fax Class 2.1 is an enhanced version of Class 2.0, which is backwards compatible with software designed for Class 2.0.

How to confirm which Fax Classes your installed modem supports:

1. Type "device manager" in the Start Search box, and then click Device Manager in the Programs list.
2. Expand Modems, right-click the modem that you use, and then click Properties.
   
3. On the Diagnostics tab, click Query Modem.
   
4. In the Command column, locate AT+FCLASS=?, and then note the value in the Response column.

Note: If the Response column contains a value of 1, 2, or 2.0, the modem supports Class 1, Class 2, and Class 2.0, respectively.

Class 2 and Class 2.0 are NOT the same protocols, and it is important to configure the fax software based on which protocol is supported by the modem. Class 2.1 is software compatible with Class 2.0, so if the fax modem supports Class 2.1 you can specify Class 2.0 in the software.

Enabling Fax Class 2 or Class 2.0 in Microsoft Fax

Warning: Serious problems might occur if you modify the registry incorrectly by using Registry Editor or by using another method. Modify the registry at your own risk.

1. Click Start, Type "regedit" in the Start Search box, and then click RegEdit in the Program list.
2. .Locate and then click the following registry subkey:
   HKEY_LOCAL_MACHINE\Software\Microsoft\Fax\Devices
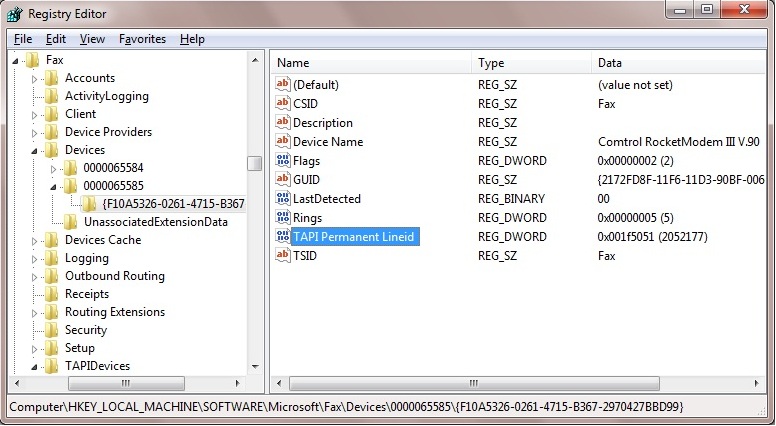
3. Expand the Devices subkey, then expand each device number and examine the subkey within it, until you find the Device Name of the desired Modem driver.
   (In the image below, a device named "Comtrol RocketModem III V.90" is shown.
4. Make note of the TAPIPermenent Lineid for this device, which is an 8 digit Hexadecimal number prefixed with "0x".
   (in the image below, the hexadecimal number is 001F5051)
   
   
   
   
   
   
5. Expand TAPIDevices in the left column, and look for the previos TAPIPermenent Lineid hexadecimal number within it.
6. If the hexidecimal number exists, expand it and click on the Modem subkey to view the TAPI settings of this modem device as seen below. It will only exist if the Microsoft Fax service has already attempted to send a fax using this modem device (atfer this modem driver was installed).
   
   
   
   
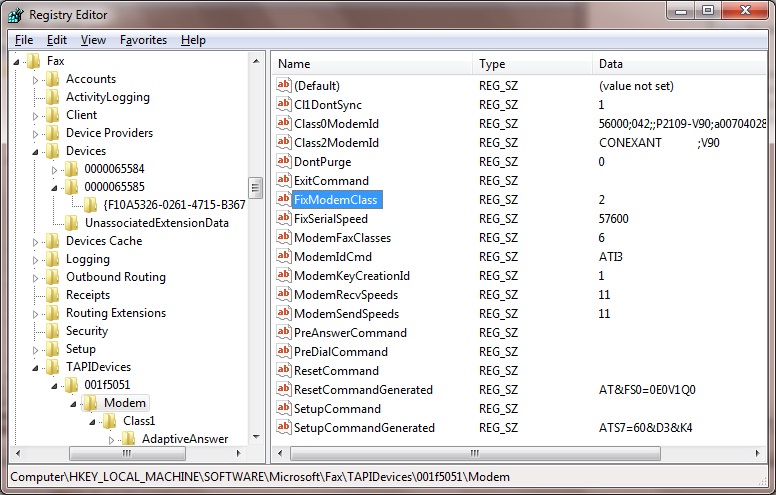
7. In the left column, right-click FixModemClass, and then click Modify.
   
8. In the Value data box, type one of the following, depending on the class that you want to set:
     The default value is "1", which sets the fax modem to use Class 1.
     Change it to "2" to set the fax modem to use Class 2, or
     Change it to "20" to set the fax modem to use Class 2.0.
   
9. If there is also a field named FaxClass, then click Modify and also change it to the same value.
   
10. Exit the Registry Editor.
    
11. Restart the fax service if it is already started. To do this, click Start, type "Services" in the Start Search box, and then click Services in the Programs list. In the Services list, right-click on Fax, and then click Restart if it is available. If the Fax service is not already started then ignore this step.

  See also: Troubleshooting Windows Fax and Scan